لوحة 4: رسم واظهار حالة تقاطع بين اسطوانة دائرية قائمة وسقف مائل بطية واحدة
=====================================================================
لوحة 4: رسم واظهار حالة تقاطع بين اسطوانة دائرية قائمة وحجم بسقف مائل بطية واحدة
 |
| الشكل1: الصورة المرفقة تبين الحد الادنى من المستويات المساعدة التي تسمح بايجاد النقاط المهمة لاهليج التقاطع بين الاسطوانة والسقف المائل، بغض النظر عما هو مرئي او مخفي، او كما لو ان كل شيء شفاف 100% - المستوى 1، يسمح بايجاد نقطتي ادنى واقصى ارتفاع للاهليج والتي تنتميان لخط اقصى انحدار - المستوى 2 يسمح بايجاد القطر الافقي (المتزاوج لخط اقصى انحدار) للاهليج - المستوى 3 يسمح بايجاد نقاط المماس بين الاهليج والكفاف الظاهر للاسطوانة زيارة الرابط المرفق للاطلاع على الاجراء الهندسي الذي كتبته في ويكيبيديا والذي يصف كيفية تحديد الاقطار الرئيسية للاهليج بدءا من قطرين متزاوجين |
 |
| الشكل 2- من اعداد الطالبة سماء زيادة - شعبة 1 |
 |
Nadia Abujbarah |
 |
Gardinia Yaghi
|
 |
 |
Malak AL Bishtawi |
أرشيف
 |
| الشكل 2: لوحة 5-2 (بالادوات) |
ملاحظات متكررة
- وبالاشارة الى الاكسنومتري هناك أخطاء في تحديد اهاليج التقاطع
- خطوط اقصى انحدار لسطح مستوي تكون دائما متورازية فيما بينها ولتحديد خط اقصى انحدار m لمستوى معين (مثلا جاما)، نقوم بما يلي: 1- نحدد الاسقاط الاول لخط افقي ينتمي للمستوى جاما ، في هذه الحالة ذلك الخط يمكن ان يكون الاثر الاول للمستوى جاما 2- نرسم الاسقاط الاول (m1) لخط اقصى انحدار للمستوى جاما بحيث يكون عمودي على ذلك الخط الافقي 3- نسقط الخط m1 على المستوى جاما وهكذا نحصل على الخط m الذي يمثل اتجاه جميع خطوط اقصى انحدار لنفس المستوى
- عمل لوحة الرسم الحر (5-1)
- رسم الخطوط المتقطعة للاشارة إلى الأجزاء غير المرئية
- رسم الخطوط المتوازية بشكل مقبول
- تظليل المستويات كما هو مبين في الشكل 1
- كتابة الترويسة كاملة في اسفل اللوحة على سطر واحد (اسم المادة ورقم الشعبة واسم المدرس واسم الطالب ورقمه الجامعي ورقم اللوحة
- استكمال أو توضيح بعض الخطوط الفعلية المرئية التي يجب ان تكون مرسومة بخط مستمر سميك
- استكمال أو توضيح بعض الخطوط الفعلية الغير مرئية التي يجب ان تكون مرسومة بخط متقطع سميك
- رسم أو استكمال خطوط اقصى انحدار (بخط اقل سمكا من الخطوط الفعلية)
- استكمال أو تعديل التقاطع المطلوب
- رسم الخطوط الإنشائية بخط مستمر رفيع
- اعادة او تحسين الاكسنومتري
- اعادة رسم الاكسنومتري الكافاليرا الافقية (plan oblique) ا ولكن قبل ذلك يجب معرفة خصائص هذا النوع من الاكسنومتري والخاصية الرئيسية هي ان مستوى الاسقاط يكون متطابق او موازي لمستوى الارض وبالتالي فإن الاشكال التي تنتمي لمستوى الارض او لأي مستوى موازي له، تبقى بالمقاس والشكل الحقيقي مثال لذلك الدائرتين التي تمثل بالتوالي القاعدة السفلية والعلوية للاسطوانة
 |
1- الاسقاط الثاني للمحور يرسم بخط ونقطة والاسقاط الاول يكون نقطة، وبالتالي الخط الواصل بين الاسقاطين هو خط انشائي ويرسم بخط نحيف وليس متقطع
2- الاسقاط الاول لخط التقاطع بين الواجهة اليسرى ومستوى الارض يرسم بخط متقطع
3- خط الارض يرسم بخط سميك
|
 |
اعادة رسم الاكسنومتري الكافاليرا الافقية (plan oblique)
ا ولكن قبل ذلك يجب معرفة خصائص هذا النوع من الاكسنومتري والخاصية الرئيسية هي ان مستوى الاسقاط يكون متطابق او موازي لمستوى الارض وبالتالي فإن الاشكال التي تنتمي لمستوى الارض او لأي مستوى موازي له، تبقى بالمقاس والشكل الحقيقي مثال لذلك الدائرتين التي تمثل بالتوالي القاعدة السفلية والعلوية للاسطوانة
|
 |
1- يرسم الخط الانشائي بخط نحيف
2- الانتباه الى ما هو مرئي وما هو لامرئي بالنسبة للكفاف الظاهر للاسطوانة
3- كما الملاحظة 1
4- المسافات بين اسقاطات رواسم الاسطوانة تصغر كلما اقتربت من الكفاف الظاهر
5- خطأ في تقابل نقاط الاسقاط الاول ونقاط الاسقاط الثالث
6 - وبالاضافة الى ذلك يجب استخدام الكافاليرا الافقية (plan oblique) لعمل الاكسنومتري
|
 |
| Sally Daghlasالرسم والاظهار المعماري (Arch. Drawing & Representation ) |
 |
| شكل 1: لوحة 5-1 (رسم حر) |
من المهم مطالعة الروابط التالية
- رابط اللوحة 2 التي يتناول الاسقاطات العمودية والاكسنومتري لحالة تقاطع بين خط رأسي ومستوى مائل موازي لخط الارض http://disegno-e-rappresentazione-arch-ju.blogspot.com/2017/01/1.html
- البحث عن
- حالة تقاطع بين اسطوانة دائرية ومستوى مائل
https://www.google.com/search?q=%D8%AD%D8%A7%D9%84%D8%A9+%D8%AA%D9%82%D8%A7%D8%B7%D8%B9+%D8%A8%D9%8A%D9%86+%D8%A7%D8%B3%D8%B7%D9%88%D8%A7%D9%86%D8%A9+%D8%AF%D8%A7%D8%A6%D8%B1%D9%8A%D8%A9+%D9%88%D9%85%D8%B3%D8%AA%D9%88%D9%89+%D9%85%D8%A7%D8%A6%D9%84&tbm=isch&tbo=u&source=univ&sa=X&ved=0ahUKEwiH6qvdhM7bAhVML8AKHTWyCwgQsAQIJA&biw=1366&bih=598
https://www.google.com/search?q=%D8%AD%D8%A7%D9%84%D8%A7%D8%AA+%D8%AA%D9%82%D8%A7%D8%B7%D8%B9+%D8%A8%D9%8A%D9%86+%D8%AE%D8%B7+%D9%88%D9%85%D8%B3%D8%AA%D9%88%D9%89+%D9%85%D8%A7%D8%A6%D9%84&source=lnms&tbm=isch&sa=X&ved=0ahUKEwid84Wf4LfbAhWKalAKHR-MCmYQ_AUICigB&biw=1366&bih=647
أعمال الطلاب
 |
Farhad Mustafa |
ارشيف
: https://www.facebook.com/groups/disegnarch/: موقع المجموعة على الفيسبوك
===========================================================
 |
| Add caption |
 |
| مجسم 4: عملية فرد الاسطوانة |
 |
أميرة حسنtoالرسم والاظهار المعماري (Arch. Drawing & Representation ) |
 |
| Nour Karaki |
 |
| Mohammad Rahhalالرسم والاظهار المعماري (Arch. Drawing & Representation |
ملاحظات متكررة
- تعديل اللوحة بشكل جذري
- استكمال أو تعديل التقاطع المطلوب
- رسم أو استكمال خطوط اقصى انحدار (بخط اقل سمكا من الخطوط الفعلية)
- رسم الخطوط المتوازية فيما بينها بشكل مقبول
- تعديل السقف المائل في الاكسنومتري و/أو في الاسقاطات العمودية
- تظليل المستويات كما هو مطلوب
- استكمال أو توضيح بعض الخطوط الفعلية المرئية التي يجب ان تكون مرسومة بخط مستمر سميك
- استكمال أو توضيح بعض الخطوط الفعلية الغير مرئية التي يجب ان تكون مرسومة بخط متقطع سميك
- رسم الخطوط الإنشائية بخط مستمر رفيع
- كتابة الترويسة كاملة في اسفل اللوحة على سطر واحد (اسم المادة ورقم الشعبة واسم المدرس واسم الطالب ورقمه الجامعي ورقم اللوحة
- رسم رواسم السطح الاسطواني بالشكل الصحيح
- رسم اهليج التقاطع بالشكل الصحيح
- رسم محور الاسطوانة بخط dash-dot
 |
| عند النظر إلى الحافة التي يرسمها الماء على جدار كأس مائل نرى قطعا ناقصا كما في حالة التقاطع بين اسطوانة دائرية وسقف مائل |
 |
| لوحة 4 (شعبة2): اسقاطات عمودية واكسنومتري كافاليرا رأسية (Cabinet) لحالة تقاطع بين ححم مغطى بسقف اسطواني وسقف مائل بطيتين |
 |
لوحة 4- شعبة 2Enas Alassi |
 |
| Enas Alassi مجسم 4 |
 |
مجد ابو عجمية |
 |
Sondos Barhomitoالرسم والاظهار المعماري (Arch. Drawing & Representation |
أرشيف
 |
| ل4: حالة تقاطع بين اسطوانة دائرية قائمة وسقف مائل بطيتين/شعبة 2 |
 |
| ل4: حالة تقاطع بين اسطوانة دائرية مائلة (او --) وسقف مائل بطية واحدة/ |
ملاحظات متكررة
- عمل لوحة الرسم الحر (4-1) أو تعديلها بشكل جذري
- استكمال أو تعديل التقاطع المطلوب
- رسم أو استكمال خطوط اقصى انحدار (بخط اقل سمكا من الخطوط الفعلية)
- رسم الخطوط المتوازية بشكل مقبول
- تعديل سمك السقف المائل في الاكسنومتري و/أو في الاسقاطات العمودية
- تظليل المستويات كما هو مبين في الشكل 1
- استكمال أو توضيح بعض الخطوط الفعلية المرئية التي يجب ان تكون مرسومة بخط مستمر سميك
- استكمال أو توضيح بعض الخطوط الفعلية الغير مرئية التي يجب ان تكون مرسومة بخط متقطع سميك
- رسم الخطوط الإنشائية بخط مستمر رفيع
- كتابة الترويسة كاملة في اسفل اللوحة على سطر واحد (اسم المادة ورقم الشعبة واسم المدرس واسم الطالب ورقمه الجامعي ورقم اللوحة
 |
| "unfolding oblique cylinder" |
 |
| مجسم 4/ شعبة 1 طريقة بديلة لعملية بسط (او فرد) الاسطوانة المائلة التي تم تبيانها سابقا، تكمن في نمذجة رواسم الاسطوانة بواسطة عيدان خشبية، وحيث يمكن تحديد طول كل عود في الإسقاط الثاني http://disegno-e-rappresentazione-arch-ju.blogspot.com/2017/02/blog-post_7.html
un metodo alternativo al sviluppo del cilindro che e' stato illustrato nella figura -- precedente, si può costruire il modello attraverso la rappresentazione delle generatrici del cilindro mediante delle stecche di legno ,la lunghezza di ciascuna stecca si può ricavare dalla seconda proiezione
|
 |
Alaa Nahar |
 |
| ل4: حالة تقاطع بين اسطوانة دائرية قائمة وسقف مائل بطيتين |
 |
Ahmad Raddadاحسنت ولكن بقي فقط رسم خطوط اقصى انحدار والتفاطع مع مستوى الارض |
 |
| Mohammed AbuEbeidالرسم والاظهار |
Case of intersection between a volume covered by a barrel vault and another volume covered with a sloped roof
محاضرة 2/21/ لوحة 4
اللوحة 4 تتناول بشكل رئيسي حالة تقاطع بين حجم مغطى بقبة اسطوانية وحجم أخر مغطى بسقف مستوي مائل. لهذا الهدف قد تم استخدام اسلوبين من أساليب الإظهار, وهما الاكسنومتري الكافاليرا الأفقية (Cavalier Perspective) و طريقة مونج (Monge projection).
 |
| شكل1: الرسمة تظهر الإنشاءات الهندسية اللازمة لتحديد اهليج التقاطع بين القبة الاسطوانية والمستوى المائل. وهذا يتم باستخدام مستويات رأسية مساعدة (باللون السماوي) بحيث تقطع الحجم المعني وفقا لمقاطع سهلة التحديد (الخطوط باللون الاحمر). كل واحد من هذه المستويات يقطع الاسطوانه وفقا لراسم ويقطع المستوى المعني وفقا لخط (قي هذه الحالة خط اقصى انحدار). واخيرا النقاط المشتركة (مثل Mv) بين الخطوط والرواسم لكل مستوى تحدد نقاط الاهليج المطلوب |
 |
|
المفاهيم المتناولة في هذه اللوحة:
- - تحديد التقاطع بين اسطوانة بمحور افقي ومستوى مائل
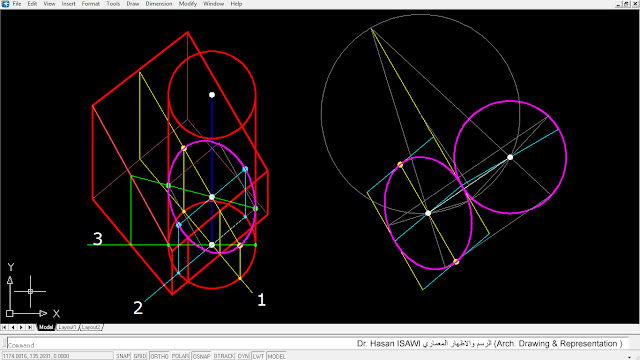
- تحديد الصورة الاكسنومترية للدائرة من خلال العلاقة التقابلية (Affinity ) التي تربط الدائرة بشكلها الحقيقي (الشكل 3).
- انشاء مستوى مائل معلومة ثلاثة نقاط منه
- انشاء قوس معلوم نقطتين وخط متماس له
- - تهشير مستوى مائل باستخدام خطوط اقصى انحدار للمستوى
- - تهشير سطح اسطواني باستخدام رواسم السطح
- - توضيح من خلال خطوط متقطعة المناطق المخفية في الإسقاطات المختلفة
- انشاء مقاطع طولية وعرضية باستخدام الاسقاطات العمودية (طريقة مونج) وبالاستعانة بالاكسنومتري الكافاليرا لفهم الحالة الفراغية المعنية.
- تحديد المقطع الاهليجي للاسطوانة
عرض متتالي لخطوات الحل الرئيسية للمسألة المعنية
في طريقة مونج (الاسقاطات العمودية)
عرض متتالي لخطوات الحل الرئيسية للمسألة المعنية
في الاكسنومتري الكافاليرا الافقية
2- تحديد الصورة الاكسنومترية للدائرة من خلال العلاقة التقابلية (Affinity ) التي تربط الدائرة بشكلها الحقيقي (الشكل 3).
العلاقة التقابلية تنشأ بين شكلين مستويين تم الحصول عليهما كاسقاطات متحدة المستوى لنفس الشكل. مثلا في الشكل 3, الدائرة والاهليج نتجا بالتوالي كصورة اكسنومترية للدائرة وكدوران لنفس الدائرة.
بشكل عام من أجل العمل في أي نوع من العلاقات التقابلية المستوية (على نفس المستوى), هناك الحاجة الى ثلاثة متطلبات, وهي
أخذين بالاعتبار أن حل المسألة الهندسية المعنية (تحديد اهليج التقاطع بين المستوى α والاسطوانة K) يمكن ان يتم من خلال استخدام عدد من المستويات المساعدة . وبهدف التبسيط ينبغي معرفة ما هو ميلان هذه المستويات للحصول على مقاطع سهلة التحديد. في هذا الصدد المستويات التي تشترك بمحور الاسطوانه تقطعها وفقا لرواسم التي هي خطوط أي انها مقاطع سهلة التحديد.
بشكل عام المستويات التي تمر بقمة الحجم سواء نهائية (مثل المخروط) او لانهائية ( مثل الاسطوانة), تقطع الحجم وفقا لرواسم. ولكن ينبغي الاخذ في الاعتبار ان من بين العدد الانهائي من المستويات التي يمكن ان تمر او توازي محور الاسطوانة, المستويات الرأسية القاطعة الاسطوانة هي الاسهل للاستخدام. وهذا بسبب سهولة تحديديها, أي انه كافي الاثر الأول للمستوى الرأسي لمعرفة وضعه في الفراغ. وفقا لهذا الاعتبار, الاجراءات في هذه الحالة لإيجاد المقطع الاهليجي يمكن ان تكون ملخصة كالتالي:
- نمرر بمحور الاسطوانة K مستوى رأسي β , حيث الاثر الاول للمستوى β يتطابق مع الاسقاط الاول لمحور الاسطوانة
- نحدد الراسم g كتقاطع بين β والاسطوانة, في هذه الحالة وبما ان محور الاسطوانة افقي, الراسم هو الذي يمر بالنقطة المفتاحية M للقاعدة النصف دائرية للاسطوانة K. أي النقطة ذو الارتفاع الاقصى للقوس الدائري.
- نحدد الخط m كتقاطع بين β والمستوى المائل α . في هذه الحالة وبما ان المستوى المساعد β عمودي على α فخط التقاطع m يمثل خط اقصى انحدار للمستوى α.
- نجد النقطة Mv كتقاطع بين الراسم g والخط m
عرض متتالي لخطوات الحل الرئيسية للمسألة المعنية
في طريقة مونج (الاسقاطات العمودية)
 |
 |
خطوة 2: تحديد الاسقاطات العمودية للقبة الاسطوانية وللاعمدة المرتكزة عليها من الجهة اليمنى (بالنظر الى الاسقاط العمودي الثالث) . في هذه المرحلة كما يلاحظ لم يحدد بعد التقاطع الاهليجي بين الاسطوانة والمستوى المائل |
 |
 |
 |
خطوة 5: تحديد الحجم الثانوي المغطى بسقف مائل موازي لمستوى سقف الحجم الرئيسي, وتحديد أيضا خطوط أقصى انحدار لهذه الأسقف |
عرض متتالي لخطوات الحل الرئيسية للمسألة المعنية
في الاكسنومتري الكافاليرا الافقية
 |
خطوة 1: تحديد الاسقاطات العمودية للحجم المغطى بسقف مائل.
|
 |
خطوة 2: تحديد الاسقاط الاكسنومتري لقاعدة القبة الاسطوانية الخارجية ومن ثم تحديد بعض الرواسم المهمة لنفس الاسطوانة. في هذه المرحلة كما يلاحظ لم يحدد بعد التقاطع الاهليجي بين رواسم الاسطوانة والمستوى المائل |
 |
 |
خطوة 4: تحديد التقاطع الاهليجي بين القبة الاسطوانية الخارجية ومستوى السقف المائل |
 |
خطوة 5: تحديد التقاطع الاهليجي بين القبة الاسطوانية الداخلية ومستوى السقف المائل, وتحديد أيضا الحجم الثانوي المغطى بسقف مائل موازي لسقف الحجم الرئيسي , وخطوط أقصى انحدار لهذه الأسقف |
2- تحديد الصورة الاكسنومترية للدائرة من خلال العلاقة التقابلية (Affinity ) التي تربط الدائرة بشكلها الحقيقي (الشكل 3).
 |
شكل 3: حالة تقابل بين الصورة الاكسنومترية للدائرة وشكلها الحقيقي |
العلاقة التقابلية تنشأ بين شكلين مستويين تم الحصول عليهما كاسقاطات متحدة المستوى لنفس الشكل. مثلا في الشكل 3, الدائرة والاهليج نتجا بالتوالي كصورة اكسنومترية للدائرة وكدوران لنفس الدائرة.
بشكل عام من أجل العمل في أي نوع من العلاقات التقابلية المستوية (على نفس المستوى), هناك الحاجة الى ثلاثة متطلبات, وهي
- - مركز التقابل (U), في هذا النوع من التقابل (Oblique affinity) المركز نقطة لانهائية باتجاه مائل بالنسبة لمحور التقابل u. مركز التقابل (U) يمثل النقطة المشتركة لجميع الخطوط (مثل الخط الأزرق في الشكل3) المارة بالنقاط المتقابلة (مثل P* P),
- محور التقابل (u) يتمثل في خط نهائي حيث تلتقي الخطوط المتقابلة (مثل الخطين باللون الاخضر الملتقية في النقطة 1),
- نقطتين متقابلتين (مثل P* P), أو خطين متقابلين (مثل P*-1, P_1).
في الحالة التي يراد فيها استخدام العلاقة التقابلية لإيجاد احدى الأشكال المتقابلة (مثل الدائرة)، ينبغي تحديد شروط العلاقة التقابلية (المذكورة اعلاة)، ومن ثم الإشراع في تحديد الشكل المتقابل الأخر (مثل الاهليج).
شروط العلاقة التقابلية في الحالة المعنية
- نوصل بواسطة خط النقطتان *P و 'P حتى يتقاطع مع محور التقابل في النقطة 2
- نوصل 2 مع النقطة المتقابلة للنقطة وهكذا نحصل على الخط المتقابل للخط السابق (خطوة 1) وحيث يتقاطع مع اتجاه مركز التقابل (باللون الأزرق) المار بالنقطة 'P نجد النقطة المطلوبة 'P , أي واحدة من نقاط الاهليج.
بطريقة مماثلة للخطوات السابقة يمكن ايجاد عدد كافي من النقاط لرسم الاهليج بطريقة دقيقة.
شروط العلاقة التقابلية في الحالة المعنية
- مركز التقابل U في هذه الحالة يمر بالنقطتين المتقابلتين C* C,
- محور التقابل u يمكن ان يكون أي خط موازي لواحد من الاقطار المتزاوجة (Conjugate Diameters) للاهليج.
- النقاط المتقابلة يمكن ان تكون 'C* C, حيث النقطة ' C تمثل مركز الاهليج (الصورة الاكسنومترية للدائرة), والنقطة C* تمثل دوران النقطة C حول محور التقابل u. أما الخطوط المتقابلة فيمكن ان تكون 'a* a. حيث الخط 'a تمثل قطر الاهليج , والنقطة *C تمثل دوران النقطة C حول محور التقابل u.
- نوصل بواسطة خط النقطتان *P و 'P حتى يتقاطع مع محور التقابل في النقطة 2
- نوصل 2 مع النقطة المتقابلة للنقطة وهكذا نحصل على الخط المتقابل للخط السابق (خطوة 1) وحيث يتقاطع مع اتجاه مركز التقابل (باللون الأزرق) المار بالنقطة 'P نجد النقطة المطلوبة 'P , أي واحدة من نقاط الاهليج.
بطريقة مماثلة للخطوات السابقة يمكن ايجاد عدد كافي من النقاط لرسم الاهليج بطريقة دقيقة.
posted by HasanIsawi @ 11:00
0 Comments
