لوحة8: القبو المتصالب الاسطواني (أو المخروطي)- المجسم اجباري كالعادة

الدكتور حسن العيسوي
الرسم والاظهار المعماري (Arch. Drawing & Representation )

اعلانات /  http://academic.ju.edu.jo/h.isawi/Lists/Announcements/AllItems.aspx
موقع المجموعة على الفيسبوك https://www.facebook.com/groups/disegnarch/

===========================================================

لتوفير الوقت والجهد وعدم التكرار من الضروري مراجعة الملاحظات المتكررة المشار اليها ادناه في هذه الصفحة والتي عليها تعتمد عمليات التقييم

مقدمة لوحة 8

من المهم مطالعة حالات تقاطع بين اسطح دورانية

لوحة8: القبو المتصالب الاسطواني (أو المخروطي)- المجسم اجباري كالعادة

unfolding بسط أو فرد سطح نصف مخروط دائري

واحدة من طرق عمل مجسم العقد المتصالب المخروطي، تكمن في معرفة كيفية فرد أو بسط واحد من المخروطين المتساويين لنفس العقد

Kawther Al-Namoora

العقد المتصالب الاسطواني= تقاطع بين اثنين من العقود الاسطوانية

التقاطع بين اثنين من العقود الاسطوانية المتساوية ينتج عقد متصالب اسطواني ، بشرط ان يكون محاورهما متحدة المستوى وأن يشكلان زاوية 90 درجة فيما بينهما

عملية فرد او بسط العقد المتصالب

الرسمة توضح كيف أن التقاطع بين اثنين من العقود الاسطوانية المتساوية ينتج عقد متصالب
بشرط ان يكون محاورهما متحدة المستوى وأن يشكلان زاية 90 درجة فيما بينهما

cross vault

http://assex.altervista.org/geometria/cefme/tav18.htm

العقد القمري  / الرسمة توضح كيف أن التقاطع بين اثنين من العقود الاسطوانية غير المتساوية ينتج عقد قمري
بشرط ان يكون محاورهما متحدة المستوى وأن يشكلان زاوية 90 درجة فيما بينهما

إجراءات نمذجة العقد المتصالب الاسطواني الدائري

نفترض ان العقدين الدائريين يتقاطعان بزواية قائمة وان واجهة احدهما (مثلا K) موازية لمستوى الاسقاط الثاني، وبالتالي فواجهة العقد الثاني تكون عمودية على مستوى الاسقاط الثاني (انظر الى الشكل 1 ادناه )
نرسم  الاسقاط الاول K1 للعقد  K  الذي يتمثل في مستطيل بمقياس 4*8 ، ومن ثم نرسم اقطار المستطيل للحصول على النقطة V التي تمثل الاسقاط الاول لنقطة التقاطع بين رواسم اقصى ارتفاع للعقدين
نرسم الاسقاط الثاني K2 للعقد  K الذي يتمثل في قوسين متحدي المركز الذي ارتفاعه 5، والمسافة بين القوسين 0.5 
وباستخدام الاجراء مونج 3d نحصل على حجم العقد K
باستخدام الايعاز ARray ننسخ العقد K مرتين بشكل دائري (Polar) من خلال تحديد النقطة V كمركز الدوران  والقيمة 90 كزاوية للدوران
باستخدام الايعاز Union نوحد العقدين ونحصل على العقد المتصالب R. 
ولكن في هذه الحالة ، وبعد أن وحدنا العقدين، ندرك أن جدارهما يغلقان الممرات ، ولحل هذه المشكلة ، فإن الخطوات اللاحقة تشرح كيفية نمذجة الاحجام الداخلية للعقود وطرحهما من تلك الجدران 
وباستخدام الايعاز Extrude نبثق حجم الفراغ الداخلي للعقد K ومن ثم نقوم بتدويره حول خط الارض بزاوية 90  درجة
وبطريقة مماثلة للخطوة 5،  ننسخ  حجم الفراغ الداخلي للعقد   K مرتين بشكل دائري (Polar) من خلال تحديد النقطة V كمركز الدوران  والقيمة 90 كزاوية للدوران.  
نوحد حجم الفراغ الداخلي للعقد   K مع نسخته الدائرية ونحصل على عقد متصالب للفراغ الداخلي، ولنسميه J
نطرح من العقد المتصالب R ، العقد المتصالب للفراغ الداخلي  J، لكي نحصل على النموذج المطلوب
نقوم بعملية اخراج اللوحة بحيث تشتمل على 3 فيوبورتات، اثنين للاسقاطات العمودية والثالث للاكسنومتري

 ملاحظات متكررة

 تعديل اللوحة بشكل جذري
استكمال أو تعديل أو اعادة تحديد التقاطع المطلوب
 رسم أو استكمال خطوط اقصى انحدار (بخط  اقل سمكا من الخطوط الفعلية)
رسم الخطوط المتوازية بشكل مقبول 
تعديل الكفاف الظاهر  في الاكسنومتري و/أو في الاسقاطات العمودية
تظليل الاسطح كما هو مطلوب في الاسقاطات وفي الاكسنومتري
 استكمال أو توضيح بعض الخطوط الفعلية المرئية التي يجب ان تكون مرسومة بخط مستمر سميك
استكمال أو توضيح بعض الخطوط الفعلية الغير مرئية التي يجب ان تكون مرسومة بخط متقطع سميك
رسم الخطوط الإنشائية  بخط مستمر رفيع
كتابة الترويسة كاملة في اسفل اللوحة على سطر واحد (اسم المادة ورقم الشعبة واسم المدرس واسم الطالب ورقمه الجامعي  ورقم اللوحة

القبو المتصالب
ينتج القبو المتصالب من تقاطع اثنين من الاسطح المخروطية ( بما في ذلك الاسطوانة كحالة خاصة للمخروط) بشرط ان يكونا متساويين ومحاورهما متحدة المستوى. بشكل عام، خط التقاطع بين اثنين من الاسطح المخروطية يكون منحنى ثلاثي الابعاد، لأنه يشارك انحناءات السطحين ؛ لكن في بعض الأحيان يكون مستويا، وهذا يحدث ، في حالة وجود مستويين متماسين لهما. 

 العقد المتصالب المخروطي= تقاطع بين اثنين من العقود المخروطية المتساوية

المرحلة الانشائية- لوحة 8

عملية البسط (unfolding) في الهندسة الوصفية تعني إمكانية بسط (أو فرد) سطح مجسم ما بحيث يصبح شكلاً مستوياً, انظر الشكل المرسوم في الأسفل.

اللوحة 8- الشعبة 2

التقاطع بين اثنين من العقود المخروطية المتساوية ينتج عقد متصالب مخروطية ، بشرط ان يكون محاورهما متحدة المستوى وأن يشكلان زاوية 90 درجة فيما بينهما

إن أبسط انواع المقاطع المخروطية (بما في ذلك الاسطوانة كحالة خاصة من المخروط)، هي الرواسم (اي الخطوط) التي يتم الحصول عليها باستخدام أي مستوى يمر برأس المخروط، وعندما يكون لدينا مخروطين متقاطعين فيما بينهما، قإن منحنيات التقاطع تحدد من خلال استخدام مستويات مساعدة تمر برؤوس تلك المخاريط. ولذلك نمرر خط بالرؤوس V وW - كما هو مبين في اللوحة المرفقة. وكل مستوى يمر بهذا الخط V-W، يقطع المخاريط وفقا لرواسم. نقاط التقاطع بين الرواسم تحدد المنحنيات المطلوبة

http://disegno-e-rappresentazione-arch-ju.blogspot.com/2017/02/6.html

Essraa Sami Hattab

Ruba Sabbagh‎الرسم والاظهار المعماري (Arch. Drawing & Representation )

Halla Mofti‎الرسم والاظهار المعماري (Arch. Drawing & Representation

Dina Wakileh

دانه إبراهيم‎الرسم والاظهار المعماري (Arch. Drawing & Representation )

Omar Otoom‎الرسم والاظهار المعماري

https://www.pinterest.com/pin/479070479097720414/

--

حالة تقاطع بين اثنين من المخاريط الدائرية

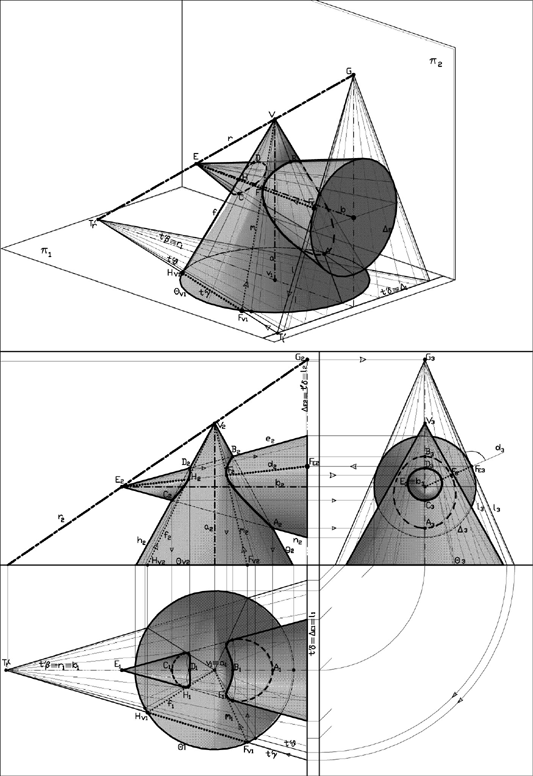تقاطع بين خروطين دائريين

طالع ايضا

109. Intersection of Two Cones having double contact with one another, that is to say, having a pair of tangent planes in common. The consequenee of their having double contact is that their curve of Intersection  breaks up into two plane ellipses. The vertices of the cones slide along a rule which turns on a universal joint. See alto model No. 114. 

110. Common Groin. Intersection of two cylinders having a pair of common tangents. The model may be set square or oblique. 

111. Intersection of Two Cylinders, one piercing the other so as to give two separate loops of intersection. 

112. Intersection of Two Cylinders, having a commou tangent, so as to give a curve having a double point at the point of contact. 

113. Intersection of Two Cylinders, neither completely piercing the other, so as to give only one loop of intersection. 114. Intersection of Two Cones, having double contact, along a pair of piane ellipses.

115. Groin. Oblique intersection of two splayed vaults of the same spring. (LINK)

---

In generale la linea comune a due superficie cilindrica è a doppia curvatura, perchè partecipa delle curvature delle due superficie; ma talvolta è piana, e ciò ha luogo, tra altri, nel caso in cui le superficie hanno due piani tangenti comuni tra loro paralleli. (LINK)

------

Presentation 12-2-2012- المحاضرة الأولى

الجامعة الأردنية / قسم هندسة العمارة
مقرر: الرسم والإظهار المعماري
المدرس: الدكتور حسن العيسوي


الفصل الدراسي الثاني 2012

ملاحظة, يرجى من الطلاب التسجيل في  الموقع المخصص  لتحميل ومناقشة  المواضيع والتمارين  المقترحة خلال المحاضرات، وهو التالي:
اسم المجموعة: الرسم والاظهار المعماري
الرابط: http://www.facebook.com/groups/233832643371047/

Slide2 

هدف مقرر الرسم والإظهار المعماري هو توفير المفاهيم والمهارات المفيدة لتطوير قدرة الطالب على تصور الأشكال الهندسية في الفراغ وبثها بطريقة سريعة وصحيحة.

عمليات الاسترداد المنظوري لإدراج مشروع افتراضي في بيئة حقيقة. ابتداء من اليسار في الأعلى يظهر موقع المشروع, ومن ثم عملية إدراج المشروع الافتراضي وأخيرا تنظيم المنطقة المحيطة.
 

Slide3

الرسم الحر والنمذجة الرقمية

القدرة على تصور وضع فراغي وترجمته إلى فكرة تصميمية معينة,  تعتبر من المهارات الضرورية للتفاعل مع المهنيين في كل مراحل المشروع.

الرسم الحر يعتبر نقطة انطلاق ضرورية نحو تقنيات النمذجة (Modeling) ثلاثية الأبعاد باستخدام الحاسوب.

Slide 4

الكيانات الهندسية الرئيسية

جميع أنواع الرسم, سواء يدوي أو رقمي (digital), تعتمد أساسا على  مفاهيم الهندسة الوصفية. التي تهتم بتدريس القواعد الاساسية لنمذجة الفراغ الهندسي وتمثيله بطريقة دقيقة لا لبس فيها.

 الكيانات الهندسية الاساسية (نقطة، خط ، مستوى) التي يتكون منها أي عنصر معماري تحدد كما يلي:

 

• النقطة, - كتقاطع بين خطين (b, d) متحدة المستوى (coplanar) ؛ - أو كتقاطع بين خط r ومستوى p1 ؛ أو كتقاطع بين ثلاثة مستويات  (p1 ,p2, p3)

• الخط , كتقاطع بين مستويين (p1 p3,)

• وأخيرا المستوى يحدد  بتعيين ثلاثة نقاط غير مصطفة على نفس الاستقامة (مثل رؤوس أي مثلث في الفراغ).

الكيانات الهندسية الرئيسية: النقطة , الخط والمستوى

Slide 5

الرسم كعملية إسقاط 

الرسم) أو الصورة(  تنتج بشكل عام من عملية إسقاط لنقاط مجسم ما على سطح مستوي (ورقة الرسم أو سطح متلقي للظل أو فيلم فوتوغرافي).

الإسقاط ينقسم إلى نوعين:

•الإسقاط الموازي (شكل1), مثل بعض أساليب الاظهار, كطريقة مونج,  والاكسنومتري (axonometry)

•الإسقاط المركزي (شكل2) , مثل المنظور بكل أنواعه (بمستوى رأسي, افقي او مائل).

الجدير بالذكر أن مصطلح الإسقاط يشير إلى عمليتين منفصلتين:

•عملية الإسقاط, تتمثل في تمرير خط بمركز الإسقاط S  وبالنقطة المعتبرة P

•وعملية التقاطع, في إيجاد نقطة الالتقاء (P*) بين الخط S  ومستوى الإسقاط.

الظلال الناتجة من مركز ضوء لانهائي تعتبر إسقاط موازي (أكسنومتري)

الظلال الناتجة من مركز ضوء نهائي تعتبر إسقاط مركزي (منظور)

Slide 6 

الاكسنومتري 

وفقا لاتجاه مركز الإسقاط (عمودي او مائل) بالنسبة لمستوى الاسقاط, الاكسنومتري تنقسم الى نوعين: الاكسنومتري العمودية والاكسنومتري المائلة.

.1الاكسنومتري العمودية, بدورها تنقسم الى ثلاثة أنواع:

• ايزومتري, حيث الزوايا بين الاسقاطات x’, y’, z’  للمحاور xyz, تكون متساوية فيما بينها (شكل5)

• ديميتري, حيث هناك تساوي بين اثنين فقط من زوايا المحاور (شكل6)

• ترميتري, حيث الزوايا بين الإسقاطات x’, y’, z’ تكون مختلفة فيما بينها (شكل7)

Slide 7

الاكسنومتري

.2الاكسنومتري المائلة, حيث اتجاة الإسقاط C∞ يكون مائل بالنسبة لمستوى الإسقاط p.  وفقا لتوازي اثنين من المحاور xyz بالنسبة لمستوى الاسقاط pالاكسنومتري المائلة تنقسم الى نوعين:

• كافاليرا افقية, حيث المستوى الأفقي (XY) يتطابق (او يوازي) مستوى الاسقاط  p (شكل9). 

• كافاليرا رأسية, حيث المستوى الرأسي yz (أو xz) يتطابق (او يوازي) مستوى الاسقاط  p (شكل10).

ميزة الاكسنومتري الكفاليرا هي أن الأشكال  المستوية الموازية لمستوى الاسقاط تبقى بشكلها ومقاسها الحقيقي حتى بعد عملية

 الإسقاط. البعد الثالث يمكن أن يبقى بمقاسه الحقيقي أو من الأفضل تقليله بأي نسبة مختارة, مثل النصف بهدف تقريب الاكسنومتري إلى التصور الطبيعي (ألمنظور).

Slide 8

الاكسنومتري الكافاليرا الأفقية 

من بين الأنواع المختلفة من الاكسنومتري , الكافاليرا الأفقية هي الأكثر استخداما في الرسم اليدوي, وذلك لسهولة وقلة الإنشاءات الهندسية المطلوبة لتمثيل الأشكال ثلاثية الأبعاد. مثلا لدينا إسقاطات مجسم مكون من متوازي المستطيلاتK (Parallelepiped) ومن هرم قائم . بحيث القاعدة العلوية لK هي أيضاً قاعدة الهرم (شكل1). لإنشاء الاكسنومتري الأفقية للمجسم, نتبع ما يلي: 

⁻نرسم القاعدة المستطيلة A1B1C1D1 بحيث يكون الضلع A1B1  دائر ب30 درجة بالنسبة لخط مرجعي (شكل2).

⁻من رؤوس القاعدة السفلية A1B1C1D1  نرسم خطوط رأسية بحيث تكون مساوية لارتفاع K. وهكذا نجد الإسقاط الاكسنومتري للقاعدة العلوية ل K.   وبالمثل نرسم أحرف الهرم بإيجاد القمة V وبتوصيلها برؤوس القاعدة العلوية  ABCD  للمتوازي K (شكل3).

Slide 9

الاكسنومتري الكافاليرا الأفقية

من الممكن أجراء تمارين أخرى لتمثيل المجسمات البدائية  في الاكسنومتري الكافاليرا الأفقية, مثل المخروط والاسطوانة والكرة والهرم والمنشور.

مثلا لتمثيل المخروط الدائري القائم , نشرع برسم القاعدة الدائرية D, ومن مركزها نرسم خط رأسي z ونعيين علية النقطة  V التي تمثل قمة المخروط. وأخيرا نرسم الخطيين المارين بالنقطة V والماسين بالتوالي قاعدة المخروط. هاذين الخطيين يمثلان الكفاف الظاهر للمخروط..

الخطوط المارة بقمة المخروط وبنقاط القاعدة

تسمى رواسم المخروط.

الميزة المهمة لهذا النوع من الاكسنومتري هي أن الأشكال المستوية الأفقية تبقى بشكلها

ومقاسها الحقيقي.

Slide 10

الاكسنومتري الكافاليرا الرأسية  

هذا النوع من الاكسنومتري أيصا يعتبر سهل الاستخدام وخصوصا في الحالات التي ينبغي فيها تمثيل منحنيات تنتمي لمستويات رأسية.

 مثلا من الأفضل تمثيل اسطوانة دائرية بمحور أفقي باستخدام هذا النوع من الاكسنومتري, لان القواعد الدائرية في هذه الحالة (الشكل المرفق) تبقي بشكلها ومقاسها ألحقيقي.

وكما هو الحال في  البوابة المقوسة، (في الشكل المرفق الآخر)، التمثيل يتم بشكل فوري.

تجدر الإشارة إلى أن خطوط العمق يمكن أن تكون بأي اتجاه بالنسبة لخط الأرض ، ويمكنها ان تبقى بمقاسها الحقيقي,  ولكن من الأفضل اختيار اي نسبة أقل (مثلا النصف).  سبب هذا  التقليل كما قلنا سبقا هو تقريب ولو جزئيا الاكسنومتري  إلى الرؤية البشرية.

 

Slide 11

نظرية الظلال

يمكن تعريف نظرية الظلال بالدراسة التي تسمح، عندما يثبت مصدر ضوء, بإنشاء، من خلال سلسلة من الإنشاءات الهندسية، الظل الذاتي والساقط لشكل ما.

الظلال في التمثيل الهندسي يمكن ان تعطي الإدراك بعمق الفراغ، أي أنها تخلق وهمية البعد الثالث على ورقة الرسم، وتعطي أيضا صورة صحيحة عن موضع الأشكال في الفراغ. ولهذا فعملية الظلال والتظليل تتطلب معرفة جيدة بقواعد الهندسة الوصفية.

Slide 12

نظرية الظلال  (theory of shadows)

الظلال تًُثري رسم السكتشات السريعة لإعطاء الفكرة الأولية لمشروع ما. والتي بعد ذلك ستحدد بدقة من خلال النمذجة الرقمية (3D modeling).

الظلال تعتبر رؤيا من مركز إسقاط أخر، أي أن هناك إسقاطين لنفس الشكل: مركز الإسقاط الأول يتطابق مع مركز النظر والأخر مع مصدر الضوء.

الظلال تسمح بإنشاء الخطة الحجمية (Volumetric plan) حيث تراكب الظل والخطة يعطي المعلومات المفقودة (مثل ألارتفاعات).

تطبيقات نظرية الظلال في طريقة مونج وفي الاكسنومتري الكافاليرا الأفقية

Slide 13

الظلال كعملية تقاطع


يمكن تفسير عملية الظل كتقاطع بين كيان ضوء وكيان متلقي للظل.
كيان الضوء يمكن ان يكون خط في الحالة التي يراد فيها إيجاد ظل نقطة (شكل1)، أو سطح مستوي عندما يراد إيجاد ظل خط مستقيم (شكل2), أو سطح منحني عندما يراد إيجاد ظل خط منحني .


مثلا ظل نقطة P على سطح α (شكل1), يمكن ان يحدد كنقطة تقاطع بين الشعاع الضوء المار بالنقطةP والسطح α المتلقي للظل.


- ظل خط مستقيم r على سطح α (شكل2), يعادل تقاطع بين مستوى الضوء المار بالخط r والسطح α.

Slide 14

الظلال الذاتية


في جميع حالات الظلال الذاتية للمجسمات البدائية التي لها قمة نهائية مثل الهرم والمخروط أو لانهائية مثل المنشور والاسطوانة, ينبغي إيجاد ظل قمة المجسم على مستوى القاعدة , ومنه رسم الخطوط الماسة لنفس القاعدة. في هذه الطريقة نجد الظل الذاتي بمجرد توصيل نقاط المماس بقمة المجسم.

الظلال الذاتية والساقطة لأسطح بقمة نهائية (مخروط, هرم) او لانهائية (اسطوانة, منشور).

Slide 15

المنظور


المنظور هو أحد تطبيقات الإسقاط المركزي, يعتبر الإظهار الهندسي الأكثر تشبيها بالرؤيا البشرية.
كما هو الحال في الإسقاط الموازي يعتمد نظرياً على عمليتين وهما عملية الإسقاط وعملية التقاطع. أي عملية إسقاط نقاط الشكل بواسطة خطوط تمر بمركز الإسقاط (في هذه الحالة نقطة نهائية) وفي عملية تقاطع هذه الخطوط مع مستوى الإسقاط. الرسم الناتج من هذا النوع من الإسقاط مشابهة للصورة الفوتوغرافية.
في هذا النوع من الإسقاط صورة الخطوط الموازية لبعضها تتشكل من خطوط تلتقي في نقطة تسمى نقطة التلاشي.

منظور بمستوى إسقاط رأسي لأحجام مكونة من
متوازيات سطوح

Slide 16

أنواع المنظور



أخذين في الاعتبار متوازي السطوح بأحرف متطابقة او موازية للمحاور xyz , يمكن تقسيم المنظور إلى ثلاثة أنواع:

1- منظور بمستوى إسقاط رأسي (أو منظور رأسي), يتميز هذا النوع من المنظور بان الصورة المنظورية للخطوط الرأسية (مثل z ( تتمثل في خطوط متوازية فيما بينها. وهذا يعني أن نقطة تلاشي هذه الخطوط تكون نقطة لانهائية.


المنظور الرأسي ينقسم بدوره إلى نوعين:


• منظور أمامي, عندما يكون مستوى الإسقاط عمودي على واحد من المحاور الأفقية (x أو y). وبالتالي منظور الخطوط العمودية على مستوى الإسقاط (مثل (x تتكون من خطوط تلتقي في النقطة الرئيسية (O0). وبالتالي صورة الخطوط الموازية لمستوى الإسقاط (مثل y وz) تتكون من خطوط متوازية فيما بينها.


• أو منظور بزاوية, عندما يكون مستوى الإسقاط موازي فقط للمحور الرأسي z.

Slide 17

أنواع المنظور

التكوينية الفراغية لمنظور بمستوى رأسي أمامي مرئي من الداخل. حيث يمكن
ملاحظة ان اتجاه خط النظر الرئيسي عمودي على واحدة من واجهات المجسم
المعتبر, وبالتالي منظورالخطوط العمودية على مستوى الإسقاط تتكون من خطوط تتلاقى في النقطة الرئيسية o0

Slide 18

العناصر الرئيسية للمنظور: مركز النظر O؛ مستوى الاسقاط p

Slide 19

منظور بمستوى أسقاط مائل

.2 منظور بمستوى إسقاط مائل (أو منظور مائل), عندما يكون مستوى الإسقاط مائل بالنسبة لمستوى الأرض xy . يتميز هذا النوع من المنظور بان إسقاطات الخطوط الرأسية تتمثل في خطوط تلتقي في نقطة تلاشي نهائية (Iz).

المنظور المائل وفقا لموضع الناظر بالنسبة للحجم المعتبر, يمكن ان يكون:

• مرئي من الأسفل (الشكل المرفق), في هذه الحالة نقطة تلاشي الخطوط تكون عادة في المنطقة العلوية من الرسم.

منظور بمستوى إسقاط مائل مرئي من الأسفل

Slide 20

• أو مرئي من الأعلى (الشكل المرفق), في هذه الحالة نقطة تلاشي الخطوط الرأسية (مثل z) تكون عادة في المنطقة السفلية من الرسم.

منظور بمستوى إسقاط مائل مرئي من الاعلى

Slide 21
طريقة مونج ( او الاسقاطات العمودية )

تعتبر واحدة من اهم اساليب الرسم والاظهار المعماري لبث المعلومات التقنية (الأشكال والقياسيات)  للمشاريع الهندسية بطريقة دقيقة. 

العناصر الرئيسية
العناصر الرئيسية لطريقة مونج,  كا هو الحال في جميع اساليب الاظهار, تعتمد على استخدام عنصرين رئيسيين وهما مركز ومستوى الاسقاط . خلافا للاساليب الاخرى, طريقة مونج تستخدم على الاقل مستويين ومركزين للاسقاط.

واحد من هذه المستويات افقي, الذي عادة ما  يتطابق مع مستوى ارض المشروع. والمستوى الاخر يكون رأسي وعادة ما يوازي الواجهة الرئيسية للمشروع.

العناصر الرئيسية في طريقة مونج

Slide 22 

في الحالة التي يستخدم فيها مستويين فقط للاسقاط, مراكز الاسقاط تكون بالتوالي:

• مركز الاسقاط الاول ∞C1, باتجاه عمودي على مستوى الإسقاط الأفقي (p1),

•   مركز الاسقاط الثاني ∞C1,  باتجاة عمودي على مستوى الاسقاط الرأسي (p2). 

خط تقاطع مستوى الاسقاط الاول p1 مع الثاني p2, يسمى خط الأرض L.L.

تمثيل مبنى بسقف مائل بطيتين, على اليمين يظهر أسلوب الاكسنومتري الكافاليرا الرأسية , وعلى اليسار طريقة مونج.

وفقا لتعقيد المبنى المعتبر, من الممكن في طريقة مونج استخدام أكثر من مستويين للاسقاط. في هذه الحالة تم استخدام مستوى اسقاط ثالث للحصول على المقاس والشكل الحقيقي للواجهة الجانبية للمبنى,

 بعد أن تتم عمليات الإسقاط يشرع في عملية دوران المستوى الرأسي حول خط ألأرض بعكس عقارب الساعة, لجعله يتطابق مع المستوي الأفقي. هدف هذه العملية هو الحصول على مستوى واحد (او بالاحرى مستويين متطابقين) لتسهيل عمليات قراءة وكتابة الرسم.
الخطوط التي توصل النقاط المتقابلة (مثلA1,A2) تسمى خطوط تناظر. التي اتجاهها يكون عمودي على خط الأرض.

  

Slide 23

تمثيل الكيانات الهندسية الرئيسية

• تمثيل النقطة 

من الممكن تحديد نقطة P في الفراغ إذا كان لدينا على الأقل إسقاطين عموديين P1 و P2 لنفس النقطة P. تقنيا نمرر بالنقطة  Pخطين عموديين على مستويات الإسقاط π2 π1 , نقطتي التقاطع P1 و P2, تمثلا بالتوالي, الإسقاط الأول P1 والإسقاط الثاني P2 للنقطة P .

بعد أن تتم عمليات الإسقاط, وبهدف تسهيل عمليات الرسم على مستوى واحد فقط,  نشرع في عملية دوران المستوى الرأسي π2  حول خط ألأرضL.L  لجعله يتطابق مع المستوي الأفقي π1  كما يظهر في الشكل.

الاسقاطات العمودية لنقطة P موضوعة في الزاوية الزوجية الأولى (angle_Dihedral )

Slide 24

تمثيل الخط

يتم تحديد الإسقاطات العمودية r1 r2  لخط r  موضوع في الفراغ, كما يلي:

- الإسقاط الاولr1   للخط r  يحدد كتقاطع بين مستوى الإسقاط π1  والمستوى الرأسي المار بالخط r؛

- وبالمثل الإسقاط الراسي r2، يحدد كتقاطع بين مستوى الإسقاط π2  والمستوى العمودي على π2  والمار بالخط r.

تقنيا، لتحديد الإسقاط الأول r1 لخط  r من الضروري تحديد وتوصيل على الأقل إسقاط نقطتين لنفس الخط r.

وبما أن الخط يعتبر كيان غير محدود في كلا الاتجاهين، فمن الممكن إيجاد تلك النقطتين كتقاطع بين الخط r ومستويي الإسقاط π2 π1 .  نقطة تقاطع r مع π1، تسمى الأثر الأول للخط r وترمز T’r . أما نقطة تقاطع r  مع π2، تسمى الأثر الثاني للخط وترمز T”r .
مثلا لإيجاد r1, نسقط الأثر الثاني T”r على p1 ومن ثم نوصله بالأثر الأول T’r. 

Slide 25

• تمثيل السطح المستوي

يتم تحديد سطح مستوي a بايجاد الاسقاطات العمودية لخطين t’a, t”a, من المستوى a.

وبما أن المستوى يعتبر نظريا كيان غير محدود, فمن الممكن إيجاد الخطين t’a, t”a , كتقاطع بين المستوى a ومستويي الإسقاط π2 π1 . الخط t”a  كتقاطع بين aوπ1. أما الخط t”a  كتقاطع بين      a وπ2 .

الإسقاطات العمودية لمستوى في وضع عام

  

Slide 26

تمثيل مستوى بواسطة ثلاثة نقاط 

من الممكن تحديد مستوى a في الفراغ إذا كان معلومة

الإسقاطات العمودية لثلاثة نقاط P,Q,R, منتمية ل a . أو

العكس, أي من الممكن ايجاد الإسقاطات العمودية لمستوى اذا

 كان معلومة ثلاثة نقاط في الفراغ ( بشرط ان لا تكون مصطفة على نفس الاستقامة.